| 问题 | 搜索算法解决八数码问题的相关信息 |
|---|---|
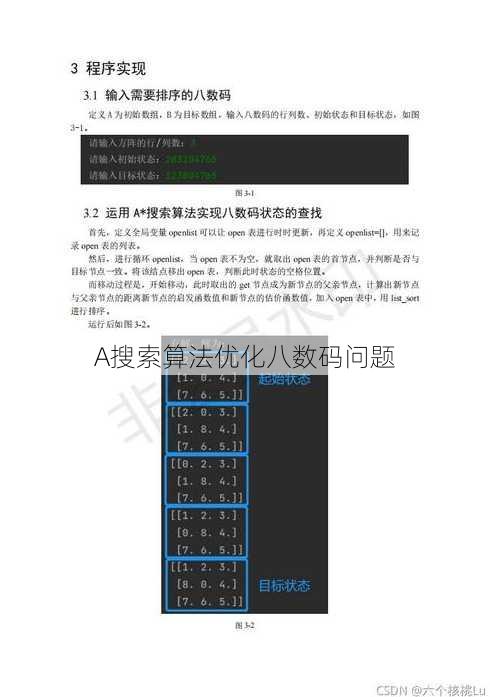
| 问题背景 | 八数码问题是经典的搜索问题,它涉及一个3x3的格子,其中包含8个不同的数字和一个空格。目标是通过滑动数字来将它们排列成特定的顺序,通常是从1到8的顺序,空格放在最后一个位置。 |
| 搜索算法 | 解决八数码问题的搜索算法有多种,包括: |
| - 宽度优先搜索(BFS):按照搜索树的宽度顺序搜索,优先访问所有相邻节点,适用于解空间较小的情况。 | |
| - 深度优先搜索(DFS):按照搜索树的深度顺序搜索,优先访问子节点,可能需要回溯,适用于解空间较大但解路径较短的情况。 | |
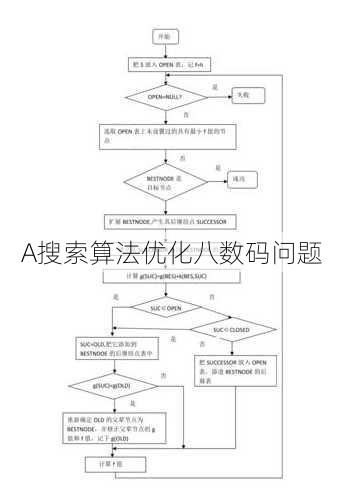
| - A*搜索算法:结合了BFS和DFS的优点,通过评估函数估计节点到目标状态的成本,优先搜索最有希望的路径。 | |
| - 迭代加深搜索(IDS):结合了BFS和DFS的迭代版本,逐步增加深度限制,直到找到解。 | |
| 评估函数 | 在A*搜索算法中,评估函数是一个关键组成部分,它通常由两部分组成: |
| - g(n):从起始状态到当前状态的代价,通常为实际移动次数。 | |
| - h(n):从当前状态到目标状态的估计代价,常用的启发式函数包括曼哈顿距离和欧几里得距离。 | |
| 解空间表示 | 解空间可以表示为一个状态空间,每个状态对应一个3x3的格子配置。 |
| 算法实现细节 | - 使用队列或栈来存储待访问的节点。 |
| - 对于每个节点,生成所有可能的移动,形成子节点。 | |
| - 使用一个数据结构(如哈希表)来存储已访问的状态,避免重复搜索。 | |
| - 对于A*搜索算法,计算每个节点的评估函数值。 | |
| 性能分析 | 搜索算法的性能取决于解空间的大小、启发式函数的质量和搜索策略。 |
| - BFS在解空间较小且深度较深时表现良好。 | |
| - DFS在解空间较大但解路径较短时表现良好。 | |
| - A*搜索算法通常在解空间较大时比BFS和DFS更高效。 | |
| 实际应用 | 八数码问题在人工智能领域被广泛研究,其搜索算法可以应用于解决其他类似的问题,如拼图游戏、路径规划等。 |

文章版权声明:除非注明,否则均为知行网原创文章,转载或复制请以超链接形式并注明出处。
